Chương 5 – Bài 7. Hình vuông trang 119 sách giáo khoa toán lớp 8 tập 1 Cánh Diều. Các em cùng Bumbii giải các bài tập sau.
1. Cho hình thoi ABCD có AC = BD. Chứng minh ABCD là hình vuông.
Giải
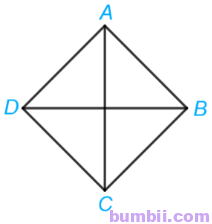
Do ABCD là hình thoi nên cũng là hình bình hành.
Hình bình hành có hai đường chéo AC và BD bằng nhau nên là hình chữ nhật.
Mà AD = AB (do ABCD là hình thoi).
Hình chữ nhật ABCD có hai cạnh kề bằng nhau (AD = AB) nên là hình vuông.
\(\)
2. Cho hình thoi ABCD có \(\widehat{A} =90^o.\) Chứng minh ABCD là hình vuông.
Giải
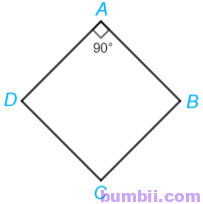
Do ABCD là hình thoi nên cũng là hình bình hành.
Lại có \(\widehat{A} =90^o\) nên hình bình hành ABCD là hình chữ nhật.
Mà AD = AB (do ABCD là hình thoi).
Hình chữ nhật ABCD có hai cạnh kề bằng nhau (AD = AB) nên là hình vuông.
\(\)
3. Cho tam giác ABC vuông tại A có đường phân giác AD. Gọi H, K lần lượt là hình chiếu của D trên AB, AC. Chứng minh tứ giác AHDK là hình vuông.
Giải
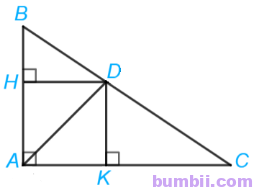
Do H, K lần lượt là hình chiếu của D trên AB, AC nên DH ⊥ AB và DK ⊥ AC
Hay \(\widehat{H} =\widehat{K} =90^o.\)
Tứ giác AHDK có \(\widehat{A} =\widehat{H} =\widehat{K} =90^o\) nên là hình chữ nhật.
Mà AD là tia phân giác của \(\widehat{HAK}\) nên AHDK là hình vuông.
\(\)
4. Cho hai mảnh giấy, mỗi mảnh có dạng hình vuông với độ dài cạnh là 1 dm. Hãy trình bày cách cắt ghép hai mảnh giấy đó để được một hình vuông có độ dài cạnh là \(\sqrt{2}\) dm.
Giải
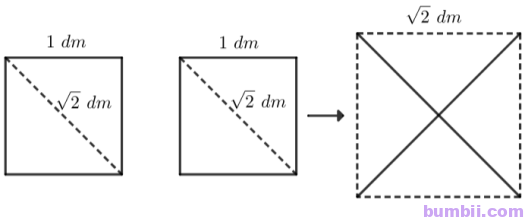
– Gấp và cắt 2 mảnh giấy hình vuông cạnh 1 dm theo đường nét đứt ta được 4 mảnh giấy hình tam giác như nhau, theo định lí pythagore đường nét đứt có độ dài \(\sqrt{2}\) dm.
– Xếp 4 mảnh giấy tam giác này sao cho đường cắt của 4 mảnh tạo thành 4 cạnh của hình vuông mới, lúc này cạnh của hình vuông mới sẽ là \(\sqrt{2}\) dm.
\(\)
5. Bạn Thảo có một mảnh giấy có dạng hình tròn. Bạn Thảo đố bạn Minh: Không dùng thước thẳng và compa, làm thế nào có thể xác định tâm của hình tròn và chọn ra 4 vị trí trên đường tròn đó để chúng là 4 đỉnh của một hình vuông?
Bạn Minh đã làm như sau:
Bước 1. Gấp mảnh giấy sao cho hai nửa hình tròn trùng khít nhau. Nét gấp thẳng tạo thành đường kính của hình tròn. Ta đánh dấu hai đầu mút của đường kính đó là hai điểm A, C.
Bước 2. Tiếp tục gấp mảnh giấy (có dạng nửa hình tròn) ở Bước 1 sao cho hai nửa mới của nửa hình tròn đó lại trùng khít nhau. Trải miếng bìa về dạng hình tròn ban đầu, ta được nét gấp mới là một đường kính khác của hình tròn.
Bước 3. Ta đánh dấu giao điểm của hai đường kính là O và hai đầu mút của đường kính mới là hai điểm B, D. Khi đó O là tâm của hình tròn và tứ giác ABCD là hình vuông (Hình 71).
Em hãy giải thích cách làm của bạn Minh.
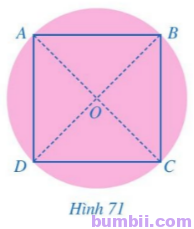
Giải
Ở bước 2, bạn Minh đã gấp mảnh giấy (có dạng nửa hình tròn) sao cho hai nửa mới của nửa hình tròn đó lại trùng khít nhau nên hai đường kính AC và BD vuông góc với nhau tại O và OA = OB = OC = OD.
Do đó AC ⊥ BD tại trung điểm O của mỗi đường.
Khi đó tứ giác ABCD là hình thoi.
Mặt khác, hai đường chéo AC và BD của hình thoi ABCD bằng nhau (do cùng là đường kính của hình tròn) nên ABCD là hình vuông có tâm là O.
\(\)
Xem bài giải trước: Bài 6. Hình thoi
Xem bài giải tiếp theo: Bài tập cuối chương 5
Xem thêm các bài giải khác tại: Giải bài tập SGK Toán Lớp 8 Cánh Diều
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech
