Bài \(4\). Hai mặt phẳng song song trang \(106\) SGK Toán lớp \(11\) Tập \(1\) Cánh diều. Các em cùng Bumbii giải các bài tập sau:
Bài \(1\). Bạn Chung cho rằng: Nếu mặt phẳng \((P)\) chứa hai đường thẳng \(a, b\) và \(a,b\) cùng song song với mặt phẳng \((Q)\) thì \((P)\) luôn song song với \((Q)\). Phát biểu của bạn Chung có đúng không? Vì sao?
Trả lời:
Phát biểu của bạn Chung không đúng vì cần thêm điều kiện hai đường thẳng \(a\) và \(b\) cắt nhau tại \(1\) điểm.
Xét ví dụ trường hợp \(a\) và \(b\) song song với nhau, cùng nằm trong \((P)\):
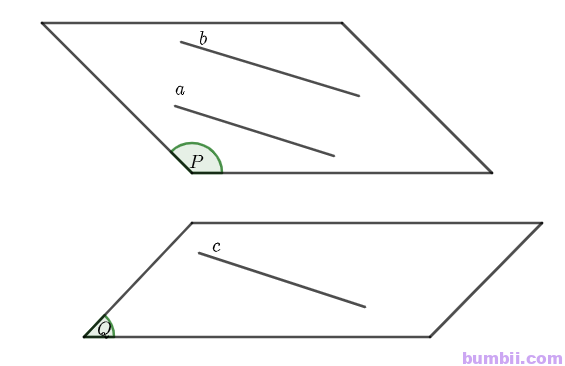
Trong ví dụ trên ta thấy, \(a\) và \(b\) cùng song với \(1\) đường thẳng \(c\) nằm trong \((Q)\) hay \(a\) và \(b\) cùng song song với \((Q)\). Tuy nhiên \((P)\) không song song với \((Q)\).
\(\)
Bài \(2\). Trong mặt phẳng \((P)\), cho hình bình hành \(ABCD\). Qua \(A, B, C, D\) lần lượt vẽ bốn đường thẳng \(a, b, c, d\) đôi một song song với nhau và không nằm trong mặt phẳng \((P)\). Một mặt phẳng cắt \(a, b, c, d\) lần lượt tại \(4\) điểm \(A’,B’, C’, D’\). Chứng minh rằng \(A’B’C’D’\) là hình bình hành.
Trả lời:
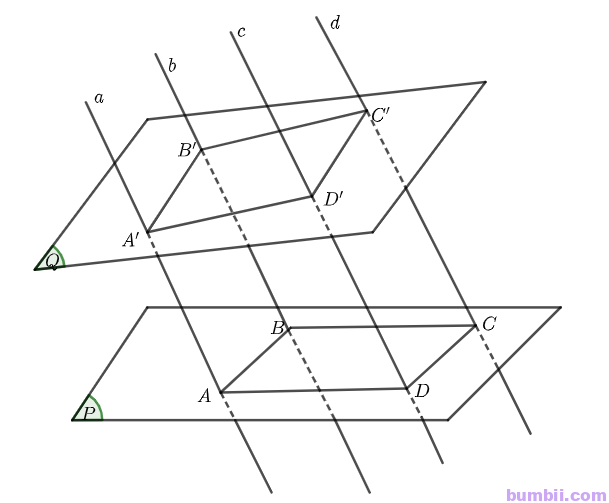
Ta có \(ABCD\) là hình bình hành nên \(AB // CD\)
\(\Rightarrow AB // (CDD’C’)\)
Lại có: \(a // d\) hay \(AA’ // DD’\)
\(\Rightarrow AA’ // (CDD’C’)\)
Mặt phẳng \((ABB’A’)\) chứa hai đường thẳng \(AA’\) và \(AB\) cắt nhau và cùng song song với \((CDD’C’)\)
Suy ra \((ABB’A’) // (CDD’C’)\)
Mặt phẳng \((Q)\) lần lượt cắt hai mặt phẳng \((ABB’A’)\) và \((CDD’C’)\) theo hai giao tuyến là \(A’B’\) và \(C’D’\).
Do đó \(A’B’ // C’D’\).
Chứng minh tương tự ta cũng được \(B’C’ // A’D’\)
Tứ giác \(A’B’C’D’\) có \(A’B’ // C’D’, B’C’ // A’D’\) nên tứ giác \(A’B’C’D\) là hình bình hành (đpcm)
\(\)
Bài \(3\). Cho tứ diện \(ABCD\). Lấy \(G_1, G_2, G_3\) lần lượt là trọng tâm của các tam giác \(ABC, ACD, ADB\).
\(a)\) Chứng minh rằng \((G_1G_2G_3) // (BCD)\);
\(b)\) Xác định giao tuyến của mặt phẳng \((G_1G_2G_3)\) với mặt phẳng \((ABD)\).
Trả lời:
\(a)\) Gọi \(M, N, P\) lần lượt là trung điểm của \(BC, CD, DB\).
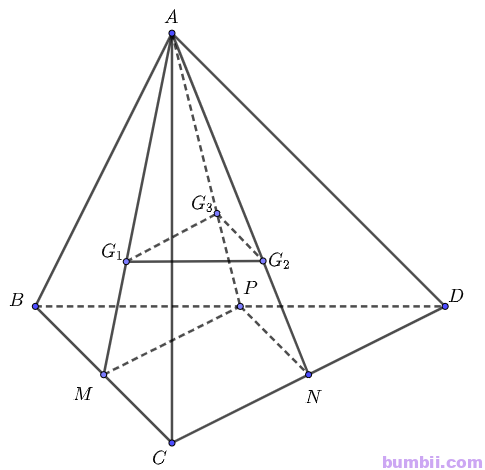
Xét mặt phẳng \((ABC)\), có \(G_1\) là trọng tâm tam giác \(ABC\) nên \(\displaystyle \frac{AG_1}{AM} = \displaystyle \frac{2}{3}\).
Xét mặt phẳng \((ACD)\), có \(G_2\) là trọng tâm tam giác \(ACD\) nên \(\displaystyle \frac{AG_2}{AN} = \displaystyle \frac{2}{3}\).
Xét mặt phẳng \((ABD)\), có \(G_3\) là trọng tâm tam giác \(ABD\) nên \(\displaystyle \frac{AG_3}{AP} = \displaystyle \frac{2}{3}\).
Trong tam giác \((AMP)\) có \(\displaystyle \frac{AG_1}{AM} = \displaystyle \frac{AG_3}{AP} = \displaystyle \frac{2}{3}\) nên theo định lí Thales đảo ta được \(G_1G_3 // MP\).
Mà \(MP \subset (BCD)\) suy ra \(G_1G_3 // (BCD)\).
Chứng minh tương tự ta cũng được \(G_2G_3 // (BCD)\).
Mặt phẳng \((G_1G_2G_3)\) chứa hai đường thẳng \(G_1G_3\) và \(G_2G_3\) cắt nhau cùng song song với mặt phẳng \((BCD)\).
Do đó \((G_1G_2G_3) // (BCD)\)
\(b)\) Ta có: \((G_1G_2G_3) // (BCD)\).
Mà \((G_1G_2G_3) \cap (ABD) = d\)
\((BCD) \cap (ABD) = BD\)
Suy ra \(d // BD\)
Mà \(G_3 \in (ABD)\) và \(G_3 \in (G_1G_2G_3)\) nên \(G_3\) là giao điểm của hai mặt phẳng \((ABD)\) và \((G_1G_2G_3)\).
Suy ra giao tuyến \(d\) của hai mặt phẳng \((ABD)\) và \((G_1G_2G_3)\) đi qua \(G_3\) và song song với \(BD\), cắt \(AB, AD\) lần lượt tại \(I, K\).
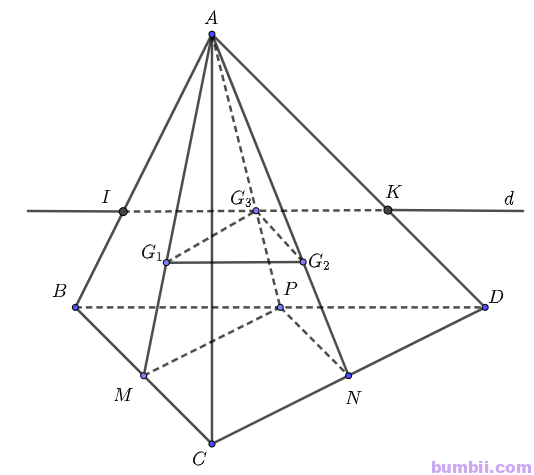
Vậy \((G_1G_2G_3) \cap (ABD) = IK\)
\(\)
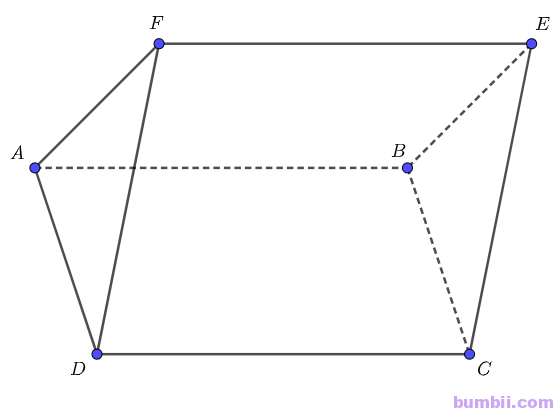
Bài \(4\). Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng.
\(a)\) Chứng minh rằng \((AFD) // (BEC)\);
\(b)\) Gọi \(M\) là trọng tâm của tam giác \(ABE\). Gọi \((P)\) là mặt phẳng đi qua \(M\) và song song với mặt phẳng \((AFD)\). Lấy \(N\) là giao điểm của \((P)\) và \(AC\). Tính \(\displaystyle \frac{AN}{NC}\).
Trả lời:
\(a)\) Ta có: \(BE // AF\) (do \(ABEF\) là hình bình hành).
Mà \(AF \subset (AFD)\)
Do đó \(BE // (AFD)\).
Lại có: \(BC // AD\) (Do \(ABCD\) là hình bình hành)
Mà \(AD \subset (AFD)\)
Do đó \(BC // (AFD)\)
Mặt phẳng \((BEC)\) chứa hai đường thẳng \(BE\) và \(BC\) cắt nhau và cùng song song với mặt phẳng \((AFD)\) nên mặt phẳng \((BEC)\) song song với mặt phẳng \((AFD)\).
\(b)\) Trong mặt phẳng \((ABEF)\), qua điểm \(M\) vẽ đường thẳng song song với (AF\), cắt \(AB, EF\) lần lượt tại \(I, H\).
Khi đó \(IH // AF\). Mà \(AF \subset (AFD)\) nên \(IH // (AFD)\)
Trong mặt phẳng \((ABCD)\), qua \(I\) vẽ đường thẳng song song với \(AD\), cắt \(CD\) tại \(K\).
Khi đó \(IK // AD\). Mà \(AD \subset (AFD)\) nên \(IK // (AFD)\)
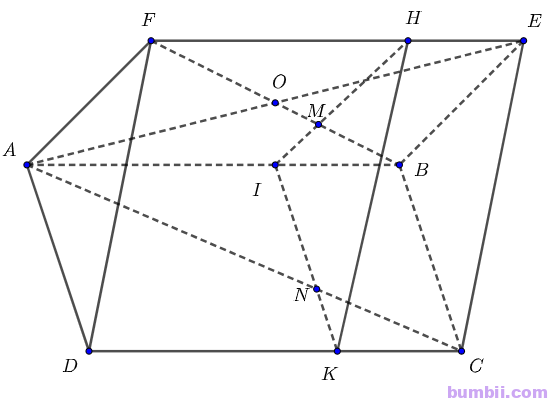
Mặt phẳng \((IHK)\) chứa hai đường thẳng \(IH\) và \(IK\) cắt nhau cùng song song với mặt phẳng \((AFD)\) nên mặt phẳng \((IHK)\) song song với mặt phẳng \((AFD)\).
Mà \(M \in IH, IH \subset (IHK)\) nên mặt phẳng \((P)\) đi qua \(M\) và song song \((AFD)\) chính là mặt phẳng \((IHK)\)
Trong mặt phẳng \((ABCD), AC\) cắt \(IK\) tại \(N\). Khi đó \(N\) chính là giao điểm của \(AC\) và mặt phẳng \((P)\).
Xét tam giác \(ABC\) có \(IN // AD // BC\) nên ta có:
\(\displaystyle \frac{AN}{NC} = \displaystyle \frac{AI}{IB}\)
Gọi \(O\) là tâm hình bình hành \(ABEF\) nên \(O\) là trung điểm của \(BF\)
Khi đó \(OF = OB = \displaystyle \frac{1}{2} BF\)
Do \(M\) là trọng tâm tam giác \(ABE\) nên ta có: \(OM = \displaystyle \frac{1}{3} OB, MB = \displaystyle \frac{2}{3} OB\).
Lại có \(IM // AF\) suy ra:
\(\displaystyle \frac{AN}{NC} = \displaystyle \frac{AI}{IB} = \displaystyle \frac{FM}{MB}\)
\(= \displaystyle \frac{FO + OM}{MB} = \displaystyle \frac{OB + \frac{1}{3} OB}{\frac{2}{3} OB} = 2\)
Vậy \(\displaystyle \frac{AN}{NC} = 2\)
Bài 4. Hai mặt phẳng song Bài 4. Hai mặt phẳng song Bài 4. Hai mặt phẳng song
Xem bài giải trước: Bài 3 – Đường thẳng và mặt phẳng song song
Xem bài giải tiếp theo: Bài 5 – Hình lăng trụ và hình hộp
Xem các bài giải khác: Giải bài tập SGK Toán Lớp 11 Cánh Diều
Thông tin liên hệ & mạng xã hội:
Website: https://bumbii.com/
Facebook: https://www.facebook.com/bumbiiapp
Pinterest: https://www.pinterest.com/bumbiitech

Hạnh phúc đạt được khi bạn ngừng chờ đợi điều đó xảy ra và thực hiện các bước để biến nó thành hiện thực.